Obliczenie naprężeń w przekroju o kształcie domku

Obliczenie naprężeń w przekroju. Obliczenie naprężeń w belce wspornikowej o przekroju „domku”. Przekrój składa się z prostokąta z otworem w kształcie kwadratu oraz na prostokącie umieszczony jest trójkąt. Na podstawie podanych wymiarów oraz wartości sił zostały obliczone naprężenia w omówionym przekroju, a dodatkowo został zaprojektowany(dobrany) przekrój dwuteowy ze względu na największy moment zginający.

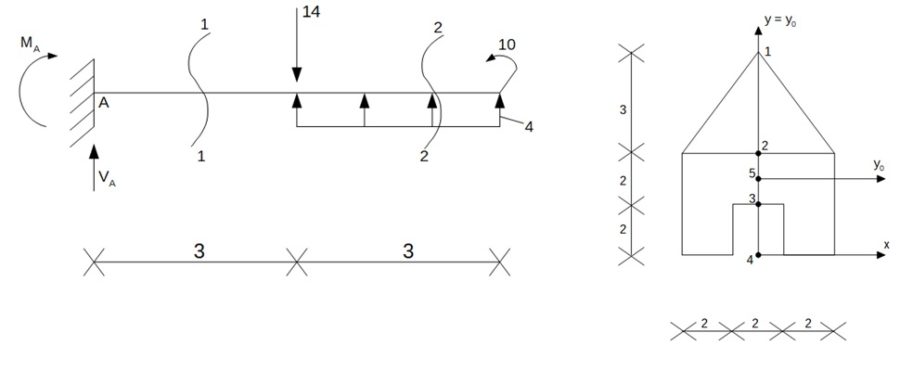
Zawartość projektu przedstawia się następująco schemat statyczny belki, obliczenie sił wewnętrznych, obliczenie charakterystyk przekroju oraz naprężeń w wymaganym punkcie belki. Dodatkowo wyznaczenie i zaprojektowanie nowego przekroju ze względu na maksymalny moment zginający. Zaczynajmy, poniżej schemat statyczny belki.

Obliczenie reakcji podporowych

\sum {y = 0} \\
{V_A} - 14 + 4*3 = 0\\
{V_A} = 2kN\\

\sum {{M_A} = 0} \\
{M_A} + 14*3 - 4*3*4,5 - 10 = 0\\
{M_A} + 42 - 54 - 10 = 0\\
{M_A} = 22kNm

Obliczenie sił wewnętrznych

Przedział 1-1     0,00m < x < 3,00m

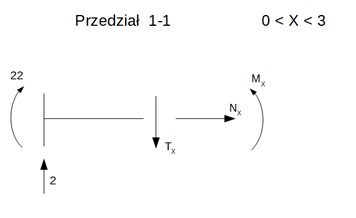
\sum {x = 0} \\
N(x) = 0kN\\

\sum {y = 0} \\
T(y) = 2kN\\

\sum {M = 0} \\
 - M(x) + 22 + 2x = 0\\
M(x) = 22 + 2x\\
x = 0\\
M(0) = 22kNm\\
x = 3\\
M(3) = 28kNm

Przedział 2-2     0,00m < x <3,00m

\sum {x = 0} \\
N(x) = 0kN\\

\sum {y = 0} \\
T(x) + 4x = 0\\
T(x) =  - 4x\\
x = 0\\
T(0) = 0kN\\
x = 3\\
T(3) =  - 12kN\\

\sum {M = 0} \\
M(x) - 10 - \cancel{4}*{x^2}*\frac{1}{x} = 0\\
M(x) = 10 + 2{x^2}\\
x = 0\\
M(0) = 10kNm\\
x = 3\\
M(3) = 28kNm

Siły wewnętrzne mamy obliczone już na całej długości belki. Nas interesują wartości w punkcie A, czyli w miejscu podpory utwierdzonej. W tym miejscu siły wewnętrzne mają następujące wartości.

N_A=0,00 kN – siły osiowe (normalne)
T_A=2,00kN – siły tnące
M_A=22,00kNm – moment zginający

Właśnie te wartości posłużą nam do obliczenia naprężeń w zdanym przekroju belki. Przypomnijmy sobie jak przekrój ten wygląda.

Właściwości geometryczne przekroju

Obliczenie środka ciężkości