Obliczanie naprężeń w przekroju złożonym
Przykład obliczenia naprężeń w belce o ciekawym przekroju, złożonym z prostokąta z wyciętym otworem oraz półkola. Belka utwierdzona na prawej krawędzi i obciążana trzema różnymi rodzajami sił. Projekt zawiera obliczenie sił wewnętrznych, następnie naprężeń oraz jako dodatek przyjęcie przekroju dwuteowego ze względu na maksymalny moment zginający. Nieobszerny projekt, zawierający obliczenia aż z trzech części bazy projektów.
Krótki opis zawartości projektu. Na ten przykład składają się następujące elementy schemat statyczny belki wraz z widocznym przekrojem tejże belki. Przed rozpoczęciem obliczania naprężeń przekrojowych zostaną też obliczone siły wewnętrzne działające w belce wraz z reakcjami w podporach. Następnie na ich podstawie obliczymy naprężenia w interesującym nas punkcie, które potem zostaną przedstawione na wykresie. Dodatkowym elementem jest zaprojektowanie stalowego przekroju dwuteowego ze względu na maksymalny moment zginający. Zaczynajmy.
Obliczenie reakcji podporowych.
\begin{array}{l}
\sum {y = 0} \\
\\
{V_A} - 3*4 - 4 = 0\\
{V_A} = 16kN\\
\\
\\
\sum {{M_A} = 0} \\
\\
{M_A} - 4*2 - 3*4*6 + 10 = 0\\
{M_A} = 70kNm
\end{array}Obliczenie sił wewnętrznych
Przedział 1-1 0,00m < x < 4,00m
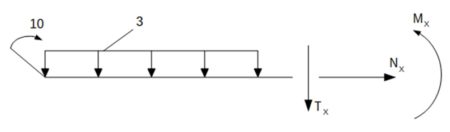
\begin{array}{l}
\sum {x = 0} \\
\\
N(x) = 0kN\\
\\
\\
\\
\sum {y = 0} \\
\\
- T(x) - 3x = 0\\
T(x) = - 3x\\
\\
x = 0\\
T(0) = 0kN\\
\\
x = 4\\
T(40 = - 12kN
\end{array}\begin{array}{l}
\sum {M = 0} \\
\\
- Mx + 10 - 3{x^2}*\frac{1}{2} = 0\\
M(x) = 10 - 1,5{x^2}\\
\\
x = 0\\
M(0) = 10knM\\
\\
x = 4\\
M(4) = - 14kNm
\end{array}Przedział 3-3 0,00m < x < 2,00m
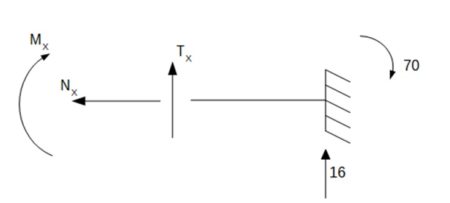
\begin{array}{l}
\sum {x = 0} \\
N(x) = 0kN\\
\\
\sum {y = 0} \\
T(x) + 16 = 0\\
T(x) = - 16kN
\end{array}\begin{array}{l}
\sum {M = 0} \\
M(x) + 70 - 16x = 0\\
M(x) = - 70 + 16x\\
\\
x = 0\\
M(0) = - 70kNm\\
\\
x = 2\\
M(2) = - 38kNm
\end{array}Przedział 2-2 2,00m < x < 4,00m
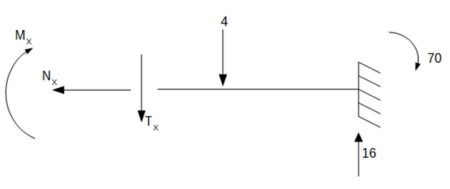
\begin{array}{l}
\sum {x = 0} \\
N(x) = 0kN\\
\\
\sum {y = 0} \\
T(x) - 4 + 16 = 0\\
T(x) = - 12kN
\end{array}\begin{array}{l}
\sum {M = 0} \\
\\
M(x) + 70 + 4*(x*2) - 16x = 0\\
M(x) = - 70 - 4*(x*2) + 16x\\
\\
x = 2\\
M(2) = - 38kNm\\
\\
x = 4\\
M(4) = - 14kNm
\end{array}Siły wewnętrzne zostały obliczone na długości całej belki. Nas interesują siły w zaznaczonym przekroju α-α, czyli w miejscu utwierdzenia belki, z obliczeń odczytujemy siły wewnętrzne działające w tym miejscu i przedstawiają się one następująco.
Nαα=0,00kN – siły osiowe (normalne)
Vαα=16,00kN – siły tnące
Mαα=70,00kNm – moment zginający
Obliczenie charakterystyk geometrycznych zadanego przekroju belki.
Środek ciężkości
Potrzebujemy tylko względem osi Y, ponieważ nasz przekrój względem osi X jest odbiciem lustrzanym. W przypadku osi X środek ciężkości znajduje się po środku długości, więc X0=3,00cm.
\begin{array}{l}
{y_0} = \frac{{(4*6*2) - (2*2*1) + \left( {\frac{{\pi *180}}{{360}}*{3^2}*5,273} \right)}}{{(4*6) - (2*2) + \left( {\frac{{\pi *180}}{{360}}*{3^2}} \right)}}
\\
\\
{y_0} = \frac{{48 - 4 + 74,5453}}{{24 - 4 + 14,1372}}\\
\\
{y_0} = 3,7cm
\end{array}Moment bezwładności względem osi X
\begin{array}{l}
I{x_0} = \left( {\frac{{6*{4^3}}}{{12}} + 24*{{( - 1,473)}^2}} \right) - \left( {\frac{{2*{2^3}}}{{12}} + 4*{{( - 2,473)}^2}} \right) + (0,1098*{3^4} + 14,137*{(1,8)^2})\\
\\
I{x_0} = (32 + 52,073) - (1,333 + 24,463) + (8,894 + 45,804)\\
\\
I{x_0} = 84,073 - 25,796 + 54,698 \\
\\
I{x_0} = 112,975c{m^4}
\end{array}Wskaźnik wytrzymałości
\begin{array}{l}
Wx_0^g = \frac{{I{x_0}}}{{{y_g}}} = \frac{{112,975}}{{3,527}} = 32,03c{m^3}\\
\\
Wx_0^d = \frac{{I{x_0}}}{{{y_d}}} = \frac{{112,975}}{{3,473}} = 32,53c{m^3}\\
\end{array}Znając już te dane, możemy przejść do obliczania naprężeń działających w przekroju α-α. Jeszcze raz przypominam jakie siły wewnętrzne działają w tym przekroju.
Nαα=0,00kN – siły osiowe (normalne)
Vαα=16,00kN – siły tnące
Mαα=70,00kNm – moment zginający
Obliczenie naprężeń normalnych
\begin{array}{l}
\delta _\alpha ^g = \frac{{\left| {{M_\alpha }} \right|}}{{W_x^g}} = \frac{{7000}}{{32,03}} = 218,55kN/c{m^2}\\
\\
\delta _\alpha ^d = \frac{{7000}}{{32,53}} = 215,19kN/c{m^2}
\end{array}Obliczenie naprężeń stycznych
\tau = \frac{{{V_2}*S{x_0}(y)}}{{I{x_0}*b(y)}}\begin{array}{l}
{V_2} = - 16,00kN\\
I{x_0} = 112,975c{m^2}
\end{array}\begin{array}{l}
{b_1} = 0,00cm\\
{b_2} = 6,00cm\\
{b_3} = 6,00cm\\
{b_3}' = 4,00cm\\
{b_4} = 6,00cm
\end{array}\begin{array}{l}
S{x_1} = 0c{m^3}\\
S{x_2} = 14,1372*1,8 = 25,45c{m^3}\\
S{x_3} = 8*2,473 = 19,784c{m^3}\\
S{x_3}' = 19,784c{m^3}\\
S{x_4} = 0c{m^3}
\end{array}Powyżej został przedstawiony wzór, który jest potrzebny do obliczenia naprężeń stycznych oraz wszystkie potrzebne dane.
\begin{array}{l}
{\tau _1} = {\tau _4} = 0N/c{m^2}\\
\\
{\tau _2} = \frac{{16000*25,45}}{{112,975*6}} = 600N/c{m^2}\\
\\
{\tau _3} = \frac{{16000*19,784}}{{112,975*6}} = 466,98N/c{m^2}\\
\\
{\tau _3}' = \frac{{16000*19,784}}{{112,975*4}} = 700,47N/c{m^2}
\end{array}Obliczone naprężenia przedstawiają się następująco na wykresie.
Jako dodatek do tego zadania, zostanie przyjęty przekrój stalowy dwuteowy ze względu na maksymalne siły zginające Mmax=70,00kNm. W skrócie, aby to zrobić należy znaleźć minimalny wskaźnik wytrzymałości potrzebny ze względu na działanie momentu o takiej wartości, a następnie należy przyjąć dwuteownik, który posiada większy wskaźnik wytrzymałości niż ten obliczony, zobaczmy.
\delta = \frac{M}{W} \le fd\left. \begin{array}{l}
M = 70kNm\\
fd = 215MPa\\
W = ?
\end{array} \right\}W \ge \frac{M}{{fd}} = \frac{{70}}{{215000}} = 3,2558*{10^{ - 4}}{m^3} = 325,58c{m^3}Widzimy, że poszukiwany jest dwuteownik o wskaźniku W (wytrzymałości) większym niż 325,58 cm3. Dlatego przyjmuję dwuteownik IPN270, którego wskaźnik wytrzymałości wynosi WIPN270=429,00cm3.
{W_x} = 429,00c{m^3} > {W_{\min }} = 325,58c{m^3}
1 Odpowiedź
[…] narysować od razu prostą prostopadłą(pod kątem 90o) do osi obojętnej, na której narysujemy wykres naprężeń. W punkcie przecięcia osi obojętnej z narysowaną prostą prostopadłą wartość naprężenia […]